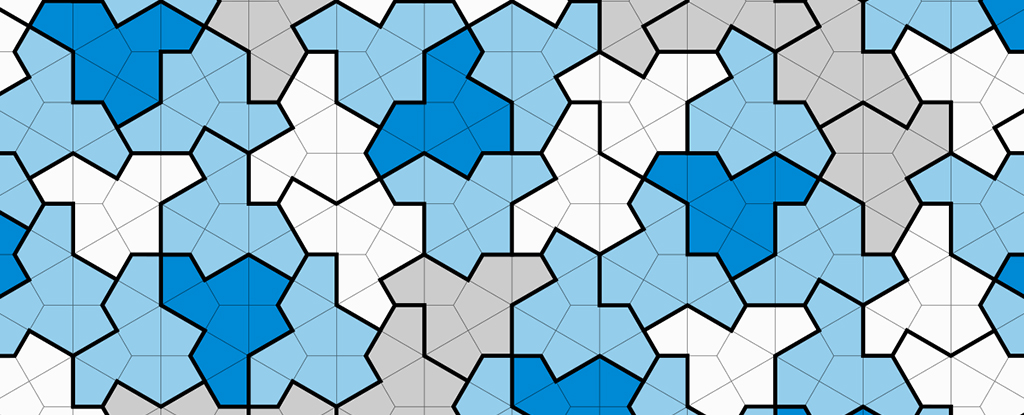
Grupa matematyków zaprezentowała nowy 13-boczny kształt, który nazwali kapeluszem.
Nie dajcie się jednak zwieść przyziemnemu opisowi. Ten kapelusz (który wygląda trochę jak fedora) to obowiązkowy element mody w nadchodzącym sezonie i można go układać w poprzek płaszczyzny, aby tworzyć niekończące się style.
Takie kształty są znane jako monady aperiodyczne lub einsteiny. Niemożliwe jest znalezienie pasującego układu lub kierunku gdzieś bezpośrednio nad lub na tym samym horyzoncie.
Kapelusz został po raz pierwszy zidentyfikowany przez nieprofesjonalnego matematyka i „formacja amatora” David Smith z Wielkiej Brytanii. Wprowadził kilka poprawek w oprogramowaniu do tworzenia kształtów, zanim przeszedł do fizycznych wycinanek z papieru.
Korzystając z pomocy naukowców z University of Waterloo w Kanadzie i University of Arkansas, Smith był w stanie udowodnić, że kształt był rzeczywiście nieokresową monadą za pomocą algorytmów komputerowych.

„Aperiodyczne grupy kwadratów poruszają się po cienkiej linii między porządkiem a chaosem, dopuszczając nachylenie, ale tylko te bez symetrii translacyjnej i nigdy nie dopuszczając prostych powtórzeń okresowego nachylenia” On pisze Członkowie zespołu w swoim artykule.
Pierwsza nieokresowa grupa płytek była Odkryta w 1966 r Składa się z 20 426 kształtów. Z biegiem lat liczba ta zmalała, a teraz jest ich znacznie więcej Aperiodyczne grupy płytek Składa się tylko z dwóch form.
Do tej pory nikt nie stworzył ani jednej płytki spełniającej standardy. Jest to coś, czego wielu matematyków szukało od lat 60., co daje wyobrażenie o znaczeniu tego odkrycia.
Kształt jest również plikiem Politekitanazwa nadana kształtom utworzonym z wielokrotności czworoboku Kształt latawca.
Według ludzi, którzy zidentyfikowali kapelusz jako nieokresowy monochromatyczny, po drodze może być więcej odkryć podobnych linii — może być więcej czekających Einsteinów (nie nazwany na cześć fizyka, ale raczej po niemiecku „jeden kamień”) być znalezionym.
„Wiele kandydujących kwadratów zostało zaproponowanych jako einsteiny, ale wszystkie z nich w jakiś sposób kwestionują pojęcia„ kafelkowania ”,„ kafelkowania ”lub„ nieokresowego ”” On pisze Badacze.
Kiedy spojrzysz na kapelusz, wydaje się to na tyle proste, że prawdopodobnie zostało znalezione wiele dziesięcioleci temu – i rzeczywiście sami badacze. nazywamy to „Prawie zwyczajny w swojej prostocie”.
Zespół przedstawił również nową metodę dowodzenia istnienia einsteinów w przyszłości, łącząc różne permutacje kształtu, aby pomóc udowodnić, że mogą one trwać wiecznie, nie stając się identycznymi w swoich wzorach.
Dopiero okaże się, w jaki sposób kapelusz będzie używany przez naukowców, matematyków i artystów w przyszłości – ale otwiera wiele możliwości eksploracji, z których nie mniej ważne jest to, czy istnieje skończona liczba nieokresowych monad. gdzieś tam, tylko czekając, aż zostaną znalezione.
„Znalezienie takiego monotile przesuwa granice złożoności, o których wiadomo, że są osiągalne dzięki zachowaniu kafelkowania pojedynczego zamkniętego dysku topologicznego” On pisze Badacze.
Artykuł opisujący nowy kształt kapelusza nie został jeszcze zrecenzowany, ale jest dostępny online pod adresem arXiv.

„Analityk. Nieuleczalny nerd z bekonu. Przedsiębiorca. Oddany pisarz. Wielokrotnie nagradzany alkoholowy ninja. Subtelnie czarujący czytelnik.”